
QUAntum SAfe Randomness
Semi-device-independent randomness from d-outcome continuous-variable detection
Journal publication available on: Phys. Rev. A 104, 062424 (2021)
Preprint available on: [arXiv:2009.08897]
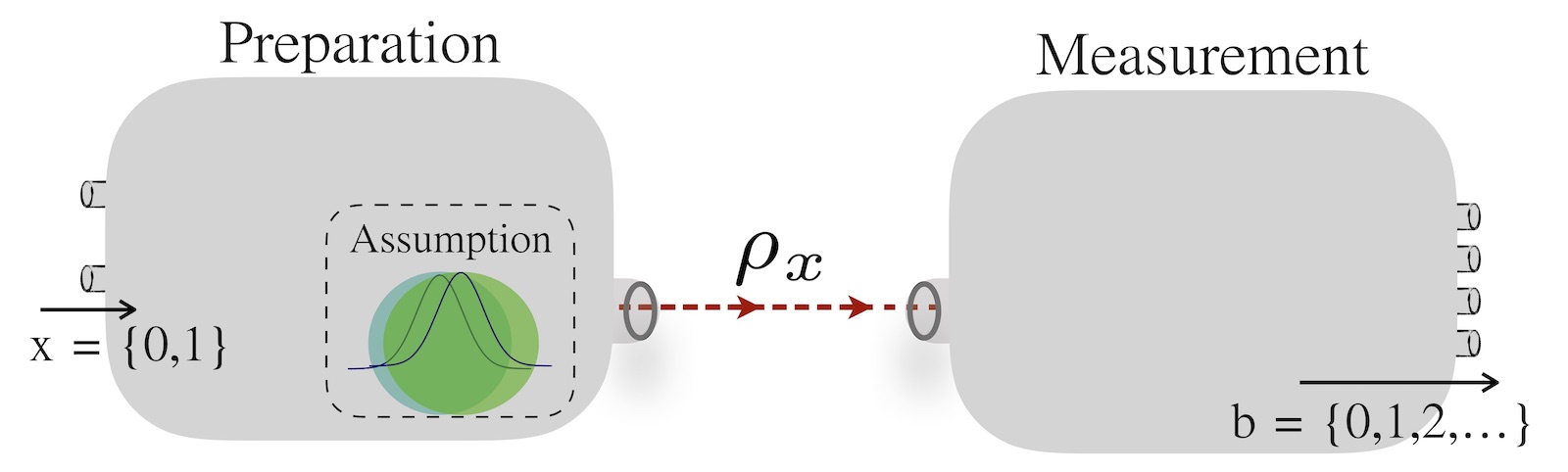
assumption is present on the state's energy.
The world of cybersecurity is developing exceedingly fast, and data encrypted by the traditional encryption methods are facing the danger of being breaked. Random numbers have always been a necessary part of every encryption system: higher quality in the random numbers implies higher security in the encrypted data. Random number generators exploits the intrinsic randomness of quantum physics. Semi-device independent (semi-DI) quantum random number generators (QRNG) offer an excellent trade-off between security, ease-of-implementation, and performance, making them a promising candidate for applications. Semi-DI QRNG certify the quantum randomness of the generated numbers by few assumptions and manageable experimental characterization of the used devices.
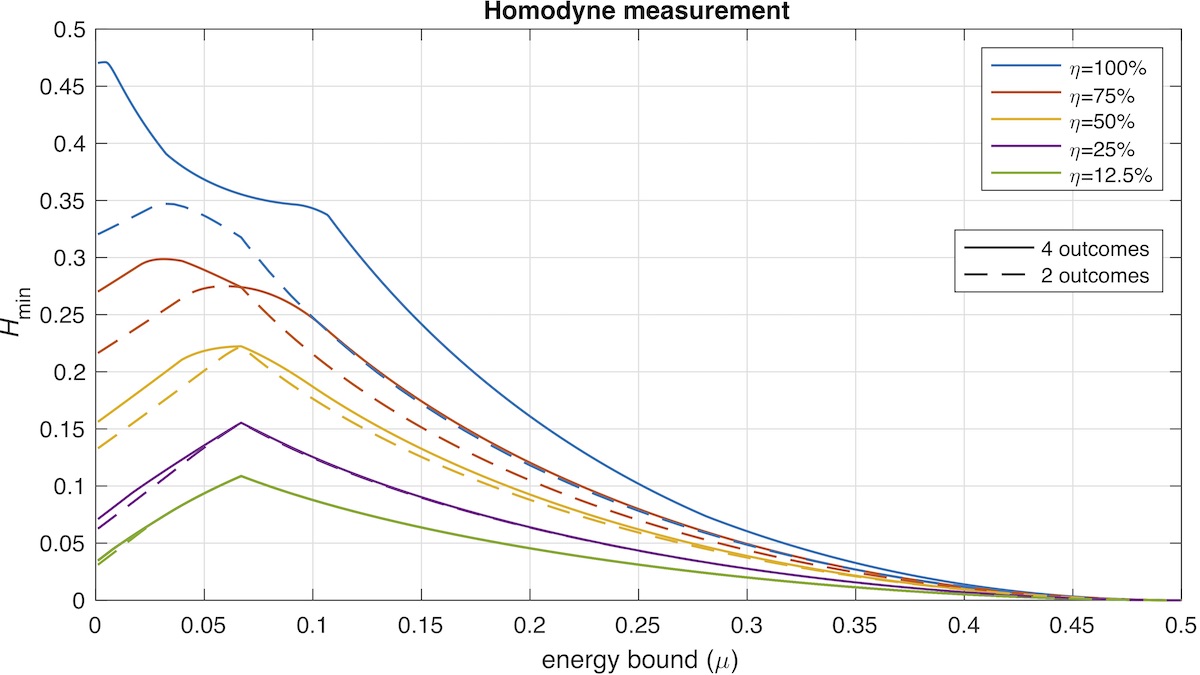
for the homodyne detector
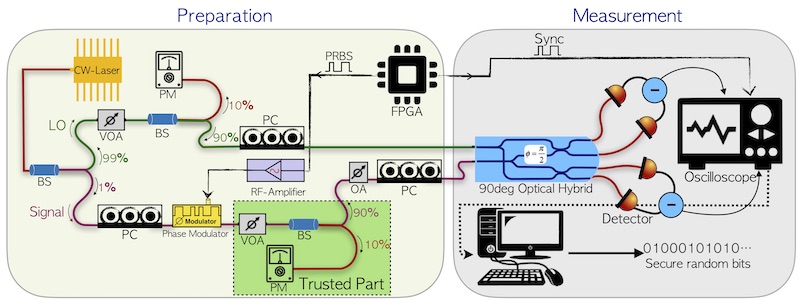
In this work, we illustrate a many-outcomes scheme with the binary phase-shift keying (BPSK) for a semi-DI protocol based on the energy assumption. The protocol is based on two untrusted devices, the preparation and measurement, and a single assumption corresponding to an upper bound on the prepared state's energy. A general scheme of this protocol is shown in the figure above. We showed that the min-entropy (namely the number of certified random bits) that can be obtained by the d-outcomes system outperforms the standard scheme (binary-outcomes). Furthermore, we compared the results of two well-known measurement schemes, homodyne and heterodyne detection. Lastly, considering the experimental imperfections, we discussed the practical feasibility of the d-outcome design. Our work shows that by using the same system, the improvement of post-processing scheme allows to certify more random numbers.

