
QUAntum SAfe Randomness
Background
True random numbers, namely unpredictable and uniformly distributed, are of fundamental importance for security applications and for scientific simulations. Any cryptographic protocol (classical or quantum) is based on the availability of random numbers. Any weakness in the random number generator is a strong asset for an attacker of any security system.
Today, the very vast majority of randomness used in cryptographic applications is generated by Pseudo Random Number Generators (PRNGs). Pseudo means that the generated numbers are not truly random but only mimic a random distribution: starting from an initial input (the so called seed), the numbers are sequentially obtained by executing a deterministic algorithm. As demonstrated by many successful attacks, PRNGs can be prone to several flaws: indeed, random numbers are always the weaker part of any encryption protocol.
The ultimate solution to generate randomness is given by Quantum Random Number Generators (QRNGs), which exploit the intrinsic randomness associated to the measurement of a physical quantum system [Rev. Mod. Phys. 89, 015004 (2017)] .
Device-Independent protocols
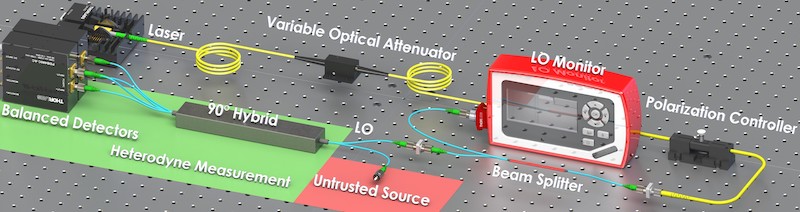
Figure from Nature Communications 9, 5365 (2018)
Typical QRNGs are realized in the "trusted-device" framework: the user trusts the devices used to realize the QRNG. In a scenario in which the privacy and the security of the generated number is a concern, any imperfection in the physical realization of the QRNG may leak information correlated with the generated numbers, the so-called side information. However, the security of trusted QRNGs fully relies on the many assumptions made on the devices and can be broken if those assumptions are not fulfilled. In contrast, device-independent (DI) protocols, by exploiting entanglement and the violation of a Bell inequality, don’t need any assumption: the violation of a Bell inequality directly bounds the min-entropy, without any assumption of the used devices (i.e. there is no need of trusting the generated state and the used measurement devices). Fully trusted QRNGs, including all the commercial ones, are easy to realize, but they require strong assumptions for their use in cryptography. On the contrary, DI protocols offer the highest level of security, but their realization is still too demanding and the achievable random generation rates are too low for practical uses [Nature 464, 1021 (2010); Nature 562, 548 (2018)].
A trade-off between security and practicality is represented by the so-called Semi-Device-Independent (SDI) protocols [NPJ Quantum Information 2, 16021 (2016)]: they allow to enhance the security with respect to standard "fully trusted" QRNGs, but they also achieve fast generation rate, dramatically larger than DI-QRNG. SDI protocols require some weaker assumptions to bound the side information with respect to fully-trusted QRNGs. Such assumptions can be related for instance to the dimension of the underlying Hilbert space, the measurement device or the source (for example the mean photon number) or the maximum overlap of the emitted states.
Photonic integrated circuits

https://photonics.lionix-international.com
Integrated circuits has attracted a lot of interest in the past years thanks to their potential for the realization of integrated photonic devices for optical communications. Indeed, it is possible to fabricate integrated high speed electro-optical modulators, high speed photodetectors and many other components required for classical optical communications.
Recently, integrated technology was also introduced in the field of quantum information: integrated silicon chips for high-speed quantum key distribution [Optica 4, 172 (2017)] and an on-chip homodyne detector for measuring quantum states and generating random numbers [Quantum Sci. Technol. 3, 025003 (2018)] were recently demonstrated.
Therefore, integrated photonic circuits offer a great potential for quantum applications due to their reduced complexity, higher robustness, and better scalability with respect to bulk or fiber optic implementations.
Quantum and Classical cryptographic applications
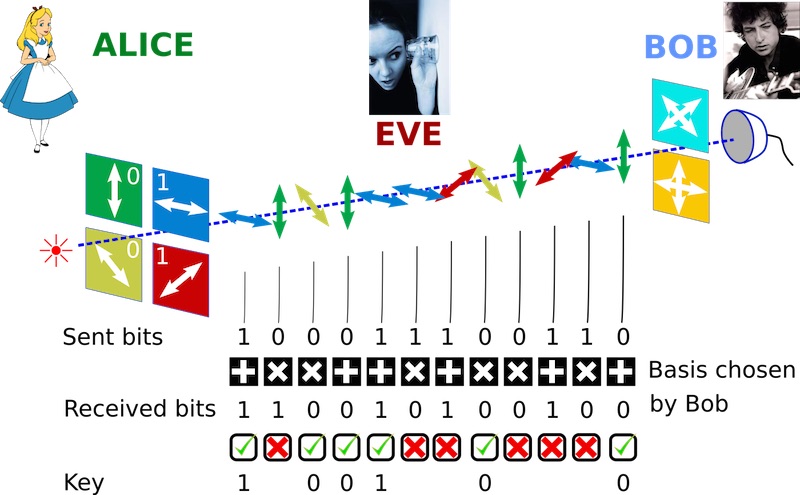
Unpredictable random numbers are indeed essential for Quantum Key Distribution (QKD) and Classical cryptographic primitives. QKD allows two users to share a secret random key by exploiting the transmission of qubit encoded into single photons (by using polarization, time, or other degrees of freedom, see the figure on the right).
QKD is unconditionally secure: the presence of an Eavesdropper can be always detected since any information extracted from the travelling photons. correspond to an increase of the Quantum Bit Error Rate. QKD (in particular the well-known BB84 protocol) is based on the assumption that Alice sends randomly four possible states that cannot be deterministically and completely distinguished. Thus, a true source of randomness is required at the transmitter: if the randomness source is not secure, the Eavesdropper may have information on the sent states and the security is compromised.
The availability of secure random numbers is of fundamental importance also for classical cryptographic applications. Triple Data Encryption Standard (Triple-DES), Advanced Encryption Standard (AES), Rivest-Shamir-Adleman (RSA) or Diffie–Hellman are well known and commonly used Cryptographic primitives that require random numbers for their implementation.